São abordadas as metodologias matemáticas de análise de percolação de Bligh & Lane, Terzaghi & Peck e Sellmeijer
Análise de percolação segundo a Creep Theory (Bligh & Lane)
A Creep Theory é uma metodologia eficiente de análise de percolação, sendo representada por equações empíricas com algum conceito teórico que incorporam as perspectivas de Bligh e Lane quanto ao piping. A perspectiva destes autores considera a ocorrência de piping ao longo de uma superfície de contato entre o maciço de um barramento e a fundação. Assim, essas teorias consideram a perda de energia como sendo linear ao longo do comprimento do contato e que o gradiente hidráulico é constante ao longo de tal contato.
Logo, como o gradiente hidráulico é dado por i=ΔH/L, esta metodologia é utilizada de forma a fornecer um comprimento seguro de percolação ao longo do contato entre fundação e maciço, fazendo com que o gradiente hidráulico da estrutura seja menor que o gradiente hidráulico crítico calculado.
Então, enquanto a equação de Bligh (Equação 1) incorpora apenas o fator horizontal do contato, a equação de Lane (Equação 2) adiciona o fator vertical como forma de reduzir o risco ao piping. Assim essas duas equações estão correlacionadas com as propriedades do solo devido a um fator característico apresentado na Tabela IX-1, onde os valores do gradiente hidráulico crítico são especificados para cada tipo de solo.

onde,
- LB é o comprimento medido ao longo do contato entre a fundação e o maciço;
- LL é o comprimento ao longo do cutoff e do contato entre a fundação e o maciço;
- lv é o comprimento na direção vertical (considera-se inclinações maiores que 45°);
- lh é o comprimento na direção horizontal (considera-se inclinações maiores que 45°);
- ∆H é a queda de potencial global do sistema;
- kv e kh é o coeficiente de permeabilidade vertical e horizontal respectivamente;
- CB é a razão creep devido a Bligh; e,
- CL é a razão creep devido a Lane.
Ressalta-se que costumeiramente, o índice kv/kh tem sido adotado como sendo 1/3.
Logo, o gradiente hidráulico é calculado através da Equação 4, onde o índice x indica se foi utilizado o fator de Bligh ou de Lane.

Tabela IX- 1 – Valor do gradiente hidráulico crítico
| Tipo de Solo | Gradiente Hidráulico de Lane | Gradiente Hidráulico de Bligh |
| Areia muito fina ou silte | 1/25,5 | 0,055 |
| Areia fina | 1/21 | 0,067 |
| Areia media | 1/18 | – |
| Areia grossa | 1/15 | 0,083 |
| Cascalho fino ou areia e cascalho | – | 0,11 |
| Cascalho médio | 1/10,5 | – |
| Cascalho grosso | 1/9 | – |
| Pedregulho, cascalho e areia | – | 0,166 to 0,25 |
| Argila | 1/6 to 1/9 | – |
Destaca-se que a abordagem adotada por Bligh e Lane ignora o fator de escala, o que acaba por indicar piping a gradientes hidráulicos menores que os valores reportados. Além disso, os valores reportados para fundações argilosas são superestimados.
Mesmo assim, tal metodologia, por ser conservadora é indicada pelo EuroCode 7 como sendo a metodologia recomendada a ser utilizada em projetos de barragens e diques.
Terzaghi & Peck
O gradiente hidráulico de Terzaghi indica que o piping ocorre quando a tensão efetiva se torna igual a zero em qualquer profundidade de areia. Assim, a Equação 5 representa o gradiente hidráulico ic de acordo com a Figura 1, que demonstra claramente o conceito de gradiente hidráulico crítico.

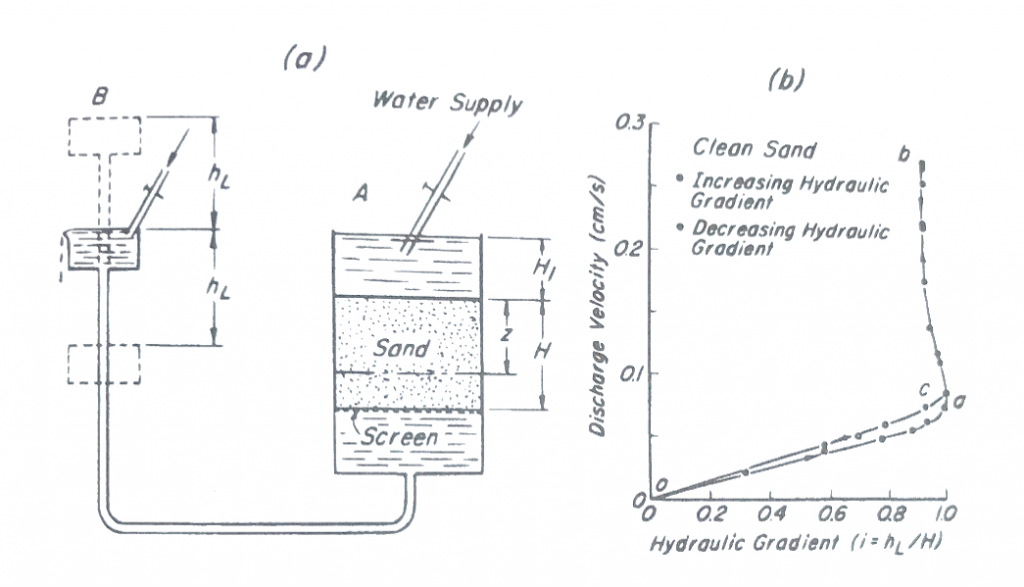
Figura 1
a) Condição hidráulica associada a um experimento de areia no qual ocorre o piping;
b) Relação entre o gradiente hidráulico e a velocidade de descarga.
Destaca-se que o critério de Terzaghi é o mais famoso método de cálculo contra o piping, mesmo que tal tenha sido concebido como um método seguro que considera o levantamento da estrutura, podendo assim não representar a realidade. Assim, a abordagem de Terzaghi considera que o piping ocorre quando as forças devido ao excesso de pressão hidrostática são superam o peso de um determinado prisma de solo, desconsiderando assim as forças cisalhantes, conforme pode ser visto pela Equação 6 e a Figura IX-2.

Outro ponto importante referente a este modelo é que o mesmo não modela as condições às quais o piping irá progredir, já que em alguns casos, mesmo que o gradiente hidráulico tenha sido atingido, a progressão do piping não ocorreu, levando assim à estabilização do sistema (ICOLD, 2015).
Logo, para superar este déficit muitos projetistas adotam que assim que o gradiente hidráulico crítico é atingido, o piping irá progredir até a ruptura da estrutura. Adicionalmente, a abordagem de Terzaghi se mostra limitada por não considerar a curva granulométrica como uma consideração do fator de segurança, já que tal fator tem grande impacto em tal evento.
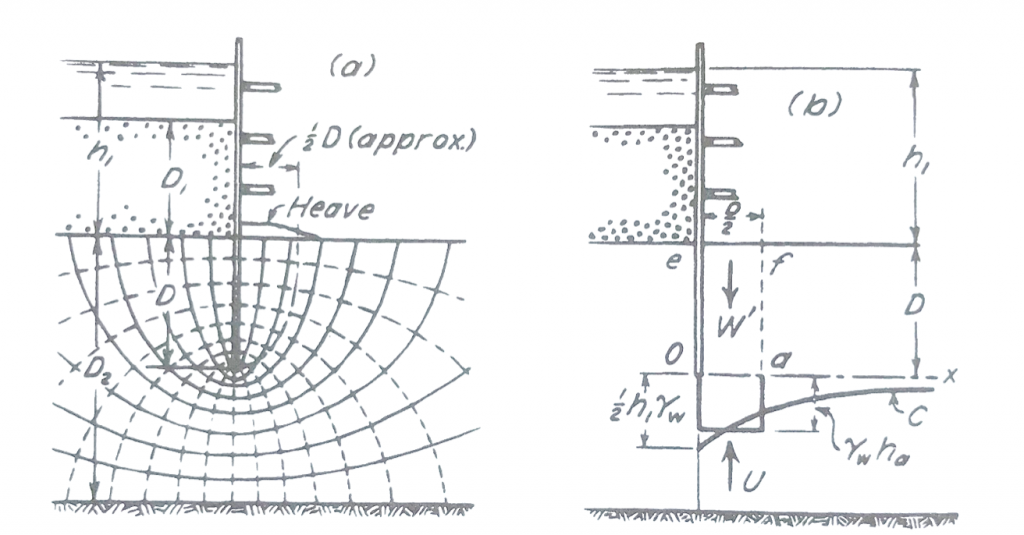
Figura 2
Fator de segurança devido ao piping em uma ensecadeira utilizando uma rede de fluxo.
a) Rede de fluxo;
b) Forças agindo na zona de potencial levantamento.
Sellmeijer Method
O método de Sellmeijer incorpora a necessidade de transporte da partícula da região a qual o processo de erosão interna regressiva está ocorrendo afim de considerar a evolução do processo. Portanto, o fluxo no interior das regiões de piping é amplamente afetado pela permeabilidade e pelos gradientes.
Dessa maneira, este método inclui três fatores principais como determinantes do gradiente hidráulico crítico. Estes fatores são: fator de resistência, dado pela Equação 8; fator de escala, dado pela Equação 9; e fator de forma geométrica, dado pela Equação 10.

onde,
- mp [m]: fator de incerteza do modelo
- H [m]: altura hidráulica ao longo da estrutura
- L [m]: comprimento de percolação (base do maciço)
- D2 [m]: espessura da camada de areia sob o maciço
- C [-]: coeficiente de erosão
- FR [-]: fator de resistência
- FS [-]: fator de escala
- FG [-]: fator de forma geométrica
- RD [%]: densidade relativa
- Cu [-]: coeficiente de uniformidade Cu = d60/d10
- KAS [%]: fator de arredondamento das partículas
- d70 [m]: diâmetro da partícula no qual 70% do peso do solo é fino
- d70m [m]: valor de calibração de referência (2.08 x 10-4 m)
- g´p [kN/m3]: peso específico saturado do solo
- G [t/m3]: densidade da partícula de solo
- gw [kN/m3] : peso específico da água
- η [-]: coeficiente de arraste de Whites (0.25)
- ϑ [DEG]: ângulo de repouso da areia
- k [m2]: permeabilidade intrínseca
onde:

- υ [m2/sec]: viscosidade cinemática
- g [m/sec2]: aceleração da gravidade
- k [m/sec]: permeabilidade hidráulica
Deve-se destacar que este método foi concebido através de 38 modelos de pequena escala. Mesmo assim, o valor do gradiente hidráulico crítico pode ser avaliado através da Figura 4, onde o fator de forma geométrica é apresentado. Entretanto, estas curvas foram obtidas considerando 37° de ângulo de repouso, coeficiente de Whites igual a 0.25, k = 1.02 x 10-7 (k) para a água a 20° Celsius e desconsiderando o fator de arredondamento das partículas e o coeficiente de uniformidade.
Deve-se ressaltar que há uma indicação de ICOLD (2015) para não se aplicar os limites expressos na Tabela 4, já que gradientes hidráulicos críticos maiores podem ser medidos em modelos de pequena escala.
Outro ponto que deve ser considerado ao se utilizar a metodologia de Sellmeijer refere-se ao fator de segurança a ser adotado. Isso pois, a equação não incorpora nenhuma margem em seus parâmetros, fazendo com que o projetista assuma tal responsabilidade.
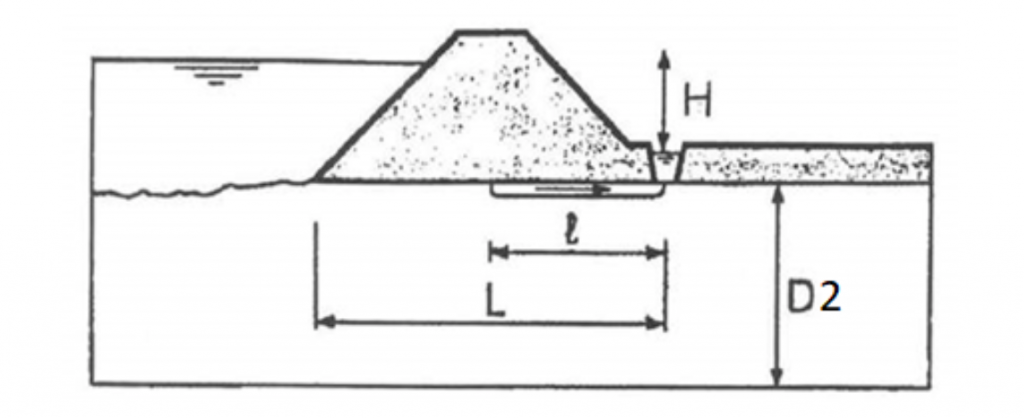
Figura 3
Ilustração da altura de água ao longo da estrutura, comprimento de percolação e espessura da camada de areia sob o maciço.
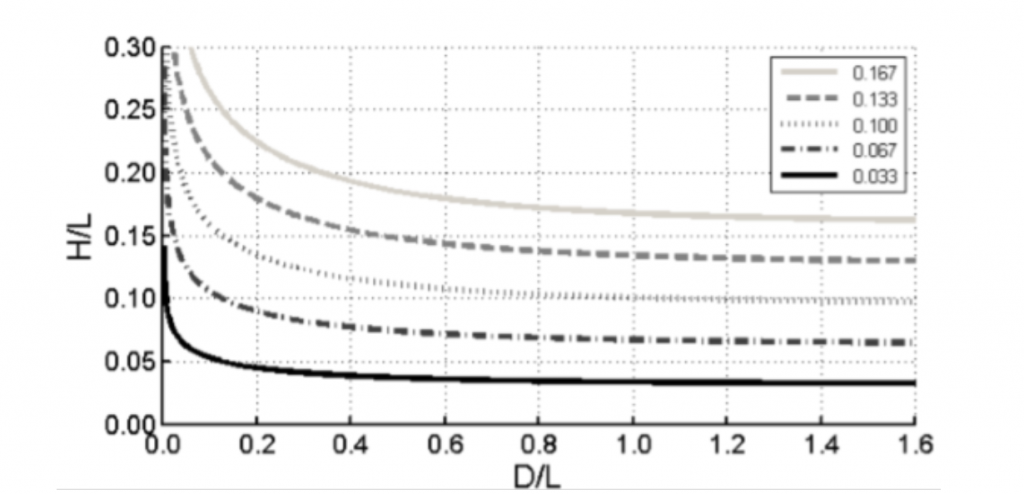
Figura 4
Gradiente hidráulico crítico para diversos valores de FR * Fs e dimensões de maciços.
Tabela 4 – Limites impostos ao método de Sellmeijer
| Parâmetro | Mínimo | Máximo | Médio |
| RD | 34% | 100% | 72.5% |
| U | 1.3 | 2.6 | 1.81 |
| KAS | 35% | 70% | 49.8% |
| d70 | 150 mm | 430 mm | 207 mm |


